نرم افزاری کاربردی و قدرتمند در زمینه محاسبات ریاضی به شمار می رود. علاوه بر محاسبات ساده ریاضیات می توان بسیاری از معادلات سنگین و بسیار سخت را با صرف کمترین زمان ممکن و در چشم به هم زدنی محاسبه نمود. این ابزار قدرتمند که بیشتر در زمینه آموزشی کاربرد دارد با دارا بودن ابزار های متعدد توانایی محاسبات و حل معادلات سنگین شیمی، فیزیک، جبر و هندسه را نیز دارد.
دانلود با لینک مستقیم:
دانلود نسخه 32 بیتی با لینک مستقیم با حجم 17 مگابایت
دانلود نسخه 64 بیتی با لینک مستقیم با حجم 18 مگابایت
منبع:https://soft98.ir
عدد پی که آن را با π نشان می دهند یکی از ثابت های ریاضی و معادل ۳٫۱۴ است. با اینکه بیشتر ما در مدرسه برای محاسبات ریاضی از عدد پی استفاده کرده ایم و می دانیم که عدد پی در واقع نسبت محیط دایره به قطره آن است اما این عدد به غیر از این تعریق مشخص، واقعیت های جالبی دارد که شاید آن را ندانید.
قضیه فیثاغورس چیست؟
قضیهٔ فیثاغورس در هندسه و فضای اقلیدسی بخشی از صورت کلی قانون کسینوس‌ها هنگامی که زاویهٔ بین دو بردار ۹۰ درجه‌است میباشد. این قضیه به نام ریاضی‌دان یونانی فیثاغورس نامگذاری شده‌است. به سخن دیگر در یک مثلث راست‌گوشه (قائم ااویه) همواره مجموع توان‌های دوم دو ضلع برابر با توان دوم وتر است.
قانون کسینوس‌ها بیان می‌کند که اگر دو بردار (یا خط) a و b در راس O تشکیل یک زاویه با نام A بدهند بردار تفاضل از رابطهٔ 
همان‌طور که می‌بینید هر گاه زاویه A برابر با ۹۰ درجه باشد مقدار 
وارون این قضیه نیز درست است، به عبارت دیگر، اگر 
راه های اثبات قضیه فیثاغورس
شما می توانید با کلیک بر روی عکس زیر این فیلم را به صورت آنلاین و مستقیم بر روی سرور وبلاگ مشاهده کنید.
 |
ریاضیات عموما مطالعه الگوی ساختار، تحول، و فضا تعریف شده است؛ بصورت غیر رسمی تر، ممکن است بگویند مطالعهاعداد و اشکال است.تعریف ریاضیات بر حسب وسعت دامنة آن و نیز بسط دامنة فکر ریاضی تغییر کرده است.
ریاضیات زبانی خاص خود دارد،که در آن به جای کلمات و علائم نقطه گذاری از اعداد و نمادها استفاده میشود. در منظر صاحبان فکر، تحقیق بدیهیات ساختارهای مجرد تعریف شده، با استفاده از منطق و نماد سازی ریاضی میباشد.
نخستین اعداد ثبت شده خطوطی بودند که روی یک چوب کشیده میشدند،که اصطلاحا آنها را چوبخط مینامیدند.این خطوط به شکل دسته های کوچک دو یا پنج تایی کشیده میشدند.سرانجام به این دسته ها نمادهای خاصی اختصاص داده شد(5،2 و غیره)و یک دستگاه حساب ایجاد شد.
ریاضیدانان نمادهای خاصی را به جای کلماتی از قبیل به اضافه و مساوی است با وضع کردند،همچنین کلمات خاصی را برای بیان مفاهیم جدید ابداع کردند.
چنانکه زمانی آن ار علم عدد ، زمانی علم فضا ، گاه علم کمیات ، و زمانی علم مقادیر متصل و منفصل خوانده اند.ریاضیات درباره حساب، هندسه ، جبر و مقابله بحث می کند که ما در اینجا به سراغ تاریخ هر یک از آنها می رویم.
ساختارهای بخصوصی که در ریاضیات مورد تحقیق و بررسی قرار میگیرند اغلب در علوم طبیعی منشاء دارند، و بسیار عمومی در فیزیک، ولی ریاضیات ساختارهای دلایلی را نیز بررسی می نماید که بصورت خالص در مورد باطن ریاضی است، زیرا ریاضیات می توانند برای مثال، یک عمومیت متحد شده را برای زیر-میدانهای متعدد، یا ابزارهای مفید را برای محاسبات عمومی، فراهم نماید. در نهایت، ریاضیدانان بسیاری در مورد مطالبی که مطالعه می نمایند که منحصرا دلایل علمی محض داشته، ریاضیات را بصورت هنری برای پروراندن علم، صرف نظر از تجربی یا کاربردی، می نگرند.
حساب ، علم اعداد است. واژه انگلیسی حساب ، از کلمه ای یونانی به معنای اعداد گرفته شده است.
در آغاز شهرنشینی ، انسان گوسفندان ، گاوها و سایر حیوانات خود را با انگشتانش می شمرد. در واقع کلمة دیژیت که برای شمارش اعداد از 0 تا 9 به کار می رود، از یک کلمة لاتین به معنای انگشت گرفته شده است.
بعدها انسان با علامت زدن روی چوب یا درخت ، اشیاء را می شمرد. اما این روش به زودی جای خود را به استفاده از علامتهایی باری هر یک از اعداد داد.
هندسه مطالعه انواع مختلف اشکال و خصوصیات آنهاست. همچنین مطالعه ارتباط میان اشکال ، زوایا و فواصـل است.
ریاضیات مملو از مسائلی است که هنوز بعد از گذشت سال‌ها بی‌پاسخ مانده‌اند؛ اما بعضی از این مسائل ظاهر بسیار ساده‌ای دارند و برای همه‌ی افراد قابل درک هستند.
در ریاضیات به مسائلی که تاکنون اثبات یا رد نشده‌اند، «مسئله‌های باز» گفته میشود. اغلب این مسائل در سطوح بالای ریاضی مطرح می‌شوند و دارای ظاهری مشکل هستند؛ مانند مسائل هزاره که حل هرکدام از آنها یک میلیون دلار به جیب شما سرازیر می‌کند؛ اما شاید اهمیت حل آنها بیشتر از جایزه باشد؛ همان‌طور که گریگوری پرلمان وقتی در سال ۲۰۰۶ یکی از مسائل هزاره را حل کرد، یک میلیون دلار را نپذیرفت. او گفت «من همه‌ی آنچه را که می‌خواهم، در اختیار دارم. من می‌توانم هستی را کنترل کنم؛ پس به من بگویید چرا باید دنبال یک میلیون دلار باشم؟».
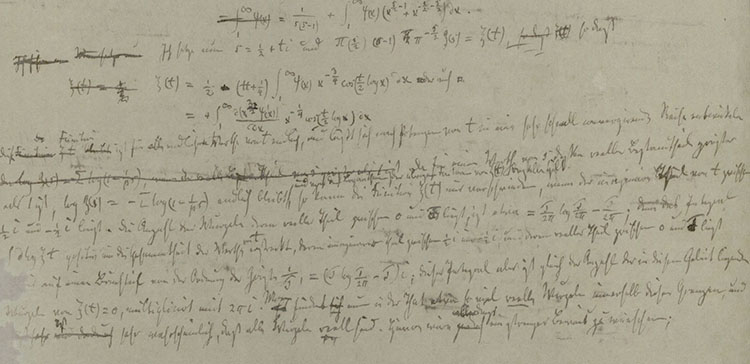
یکی دیگر از همین مسائل که به فرضیه‌ی ریمان معروف است؛ از مشهورترین و مهم‌ترین مسائل حل نشده‌ی ریاضی به شمار می‌رود که نتایجی را در ارتباط با توزیع اعداد اول در بر دارد. عکس بالا، دست‌خط ریمان را در سال ۱۸۵۹ نشان می‌دهد؛ زمانی که فرضیه‌ی مهم خود را بیان کرد. اما فارغ از تمام موارد یادشده، مسائلی وجود دارند که با وجود ظاهر ساده و قابل فهم، حل‌نشده باقی مانده‌اند؛ مسائلی که هر‌کس با دانش دبیرستانی می‌تواند آنها را درک و روی کاغذ امتحان کند. در این مقاله به هفت نمونه از مسائل این‌چنینی خواهیم پرداخت.
لطفاً برای مشاهده این 7 مسئله حل نشده به ادامه مطلب مراجعه کنید.
منبع: www.zoomit.ir
تار عنکبوت شبکه‌ای از رشته‌های پروتئینی است که توسط عنکبوتها تنیده میشود. این پروتئین سرشار از آمینو اسیدهای آلانین و گلیسین است. بیشتر رشته‌های پلی پپتیدی سازندهٔ این پروتئین، به صورت صفحات بتا آرایش یافته‌اند. این صفحات در زمینه‌ای از رشته‌های آمینو اسید به صورت صفحات آلفا جای گرفته‌اند. مارپیچ‌های آلفا با بی‌نظمی زیادی به هم پیچیده‌اند و همین بی‌نظمی باعث خاصیت کش سانی تار میشود. یکی از ویژگی‌های جالب تار عنکبوت این است که مقدار زیادی نمک و مواد ضد باکتری و ضد قارچ دارد که در برابر حملهٔ باکتری‌ها و قارچ‌ها از آن محافظت می‌کند.
کتاب روش سریع تراختنبرگ در حساب اثری است از آن کاتلر و رودولف مک شین که به توضیح روش ابداعی آسان و سریع محاسبات سنگین ریاضی توسط یاکوف تراختنبرگ پرداخته است. این کتاب در ایران توسط محمد باقری به فارسی ترجمه شده است و توسط انتشارات دانشمند در سال 1371 منتشر شده است. روش تراختنبرگ روشی برای انجام محاسبه ذهنی پایه ریاضی است که توسط یاکوف تراختنبرگ زمانی که در زندانهای نازی‌ها اسیر و تحت فشار بود برای رهایی ذهن خود از فشارها اختراع شد. این روشها شامل چندین الگوریتم انجام محاسبات است که فرد با به خاطر سپردن آنها قادر خواهد بود محاسبات پایه ریاضی را به سرعت انجام داده و بدون طی مراحل میانی به صورت مستقیم به جواب برسد.
او در سال ۱۹۵۰ مؤسسه ریاضی زوریخ را بنا نهاد که صبح‌ها شاگردان هفت الی هجده ساله و عصرها مردان و ن مشتاق در سر کلاسهای درس حاضر میشدند و از سادگی روش تازه ریاضیات لذت می‌بردند.
وی معتقد بود علت اینکه اغلب ما در کار با اعداد مشکلاتی داریم دشوار بودن فهم حساب نیست، بلکه علت آن در روش کهنه‌ای نهفته‌است که با آن به ما درس داده‌اند. مزایای مهم روش محاسبهٔ ذهنی تراختنبرگ عبارتند از سهولت و سرعت و دقت بیشتر. او تا هنگام مرگ در سال ۱۹۵۳ به تدریس این روش همت داشت .
برای دانلود با لینک مستقیم شما می توانید بر روی عکس زیر کلیک کنید.
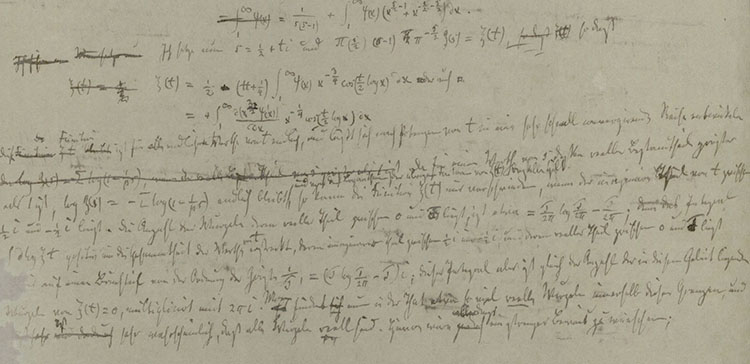
درباره این سایت